EigenVectors and EigenValues:🔗

Eigenvectors and eigenvalues are fundamental concepts in linear algebra, and they play a significant role in various machine learning algorithms. Let's dive into their definitions first, and then we'll discuss their applications in machine learning.

Definitions:🔗

1. Eigenvector: Given a square matrix $A$, an eigenvector is a non-zero vector $\mathbf{v}$ such that when $A$ is multiplied by $\mathbf{v}$, the direction of $\mathbf{v}$ doesn't change. In mathematical terms:

$A \mathbf{v} = \lambda \mathbf{v}$ where $\lambda$ is the eigenvalue corresponding to the eigenvector $\mathbf{v}$.

2. Eigenvalue: $\lambda$ is the scalar by which the eigenvector $\mathbf{v}$ is scaled (or stretched) when multiplied by the matrix $A$.

---

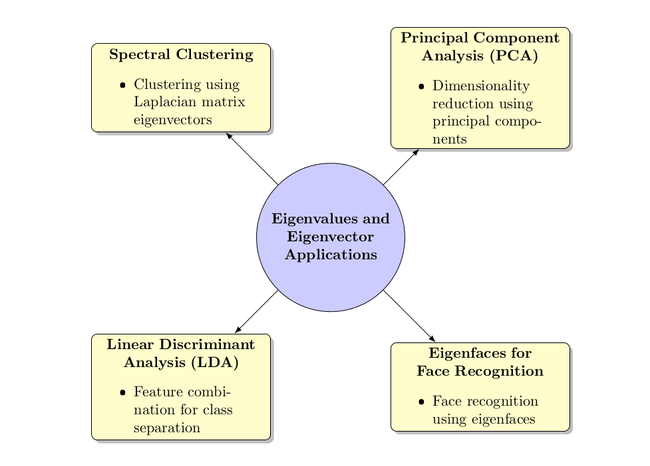
Applications in Machine Learning:🔗

1. Principal Component Analysis (PCA):

   • Problem: Dimensionality reduction. When dealing with high-dimensional data, computations become expensive, and some dimensions might be redundant or irrelevant.
   • Solution: PCA identifies the directions (principal components) in which the data varies the most. These directions are the eigenvectors of the covariance matrix of the data. The importance of each direction is determined by the corresponding eigenvalue.
   • Example: Imagine a dataset with 100 features representing different measurements of a product. Using PCA, you could reduce this to 10 features (principal components) that capture most of the variation in the data, making subsequent computations faster and models more interpretable.

2. Spectral Clustering:

   • Problem: Cluster data points into groups when traditional methods like k-means might not work well.
   • Solution: Uses the eigenvectors of the Laplacian matrix of the similarity graph of data points to cluster data.
   • Example: Imagine trying to cluster a set of data points that are arranged in two concentric circles. Traditional methods like k-means wouldn't be able to separate the circles, but spectral clustering can.

3. Linear Discriminant Analysis (LDA):

   • Problem: Find a linear combination of features that characterizes or separates two or more classes of objects or events.
   • Solution: LDA finds the eigenvectors of a matrix that maximizes the between-class scatter to within-class scatter ratio.
   • Example: In a dataset with two classes of wine, based on various features like acidity, color, and taste, LDA can find a linear combination of these features that best separates the two classes.

4. Eigenfaces for Face Recognition:

   • Problem: Recognize faces from images.
   • Solution: Represents images of faces as linear combinations of the principal components (eigenvectors of the covariance matrix of the face dataset). These principal components are called "eigenfaces."
   • Example: Given a database of face images, eigenfaces can be used to represent each face as a combination of these base eigenfaces. When a new face image is provided, it's represented in terms of these eigenfaces to find the closest match in the database.

---